|
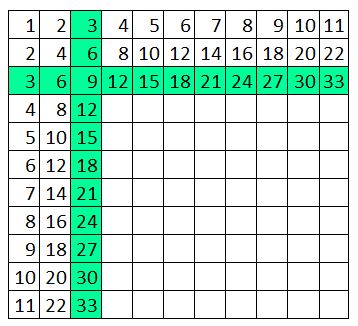
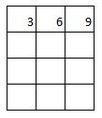
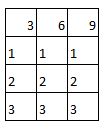
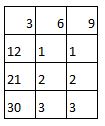
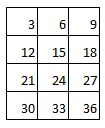
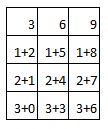
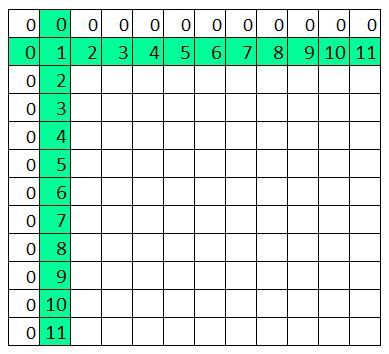
Hooray. We’ve reached a time table you don’t know off by heart. 3 6 9 12 15 18 21 24 27 30 33 I know you know bits of it, but it gets blurry in the middle. One thing you can do is secretly under your breath is to count like this One, two, THREE Four five SIX Seven, eight NINE Ten, eleven, TWELVE ... Then it forms a really nice rhythm and you’ll find yourself enjoying yourself so much you will count all the way 1068. It's quite a good way to remember the 3x table. If you get stuck is to go back to the number one and do a little quiet quiet LOUD quiet quiet LOUD chant to yourself. The LOUD bits are the three times table. Also just say the actual three times table numbers over and over to yourself. Three – Six – Nine – Twelve – Fifteen – Eighteen – Twenty-one –Twenty-four – Twenty-seven –Thirty – Thirty-three Say it ten times now. Say it ten times before bed. Try and get it so you can say it without even thinking what the words mean. Just listen to the rhythm of the words. *** *** *** *** *** *** *** *** *** *** *** A cool three times table pattern Sometimes numbers make really cool patterns. They can help you remember things, and if they don't help you remember they're just cool things to know. Try this. Step 1 Create a three by four grid. That means a table that is three columns across and four rows down. It will look like this: Step 2 In the top row, write in the first three numbers of the three times table. So the answers for 1x3, 2x3 and 3x3. You know 1x3 and 2x3 and if you can't remember 3x3 remember it's 9 which is how old you are. (You will know the 3x table by the time you are 10). Now your table will look like this: Step 3 In the second row, write 1 in every box, in the third row, write 2 in every box, in the bottom row write 3 in every box. Write the numbers to the left of the box. So now your table looks like this: Step 4 Look at the first column which has 3 in the top box. Count backwards from 3 (that is 2, 1, 0 and add that number in the next box, so the second box down has 2 in it, the third box down has 1 in it, and the bottom box has 0 in it. Now your table will look like this: Step 5 Now repeat this with the next two columns - you will be counting backwards from 6 and then from 9. Then your table will look like this: GUESS WHAT????!!!!??? That's the three times table! But wait. There's another maybe even cooler pattern for the three times table If you look at the table you just did again, there is something really cool about it. It only works for the three times table. And it only works out if you put the three times table into a table like this. Can you figure it out? Here's a hint: Now I suggest you write out this table in this pattern as soon as you arrive at anyone’s house because you never know when someone will say I have twenty seven extremely yummy treats and three children but I can’t figure out how many to give to each child so I better throw the whole lot out unless someone can quickly tell me the answer.
1 Comment
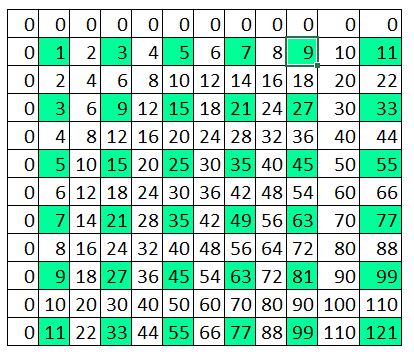
 Dear Agent AAMB So here's the thing, bozo. I heard, as well as having to learn the times table, you're having to learn division, and you think it's a total yawn. Well, sometimes you gotta learn stuff, and you might not want to learn stuff, but all the same you got to learn it. And you might think, I already know stuff so why do I have to learn more stuff? I sympathise, but when I was in a similar situation I came up with Ruby Redfort Rule Number 98: Sometimes you know more than you think you know. Take division for example. Once you know your times table you don't really need to learn division. Because you already know it. Take six times five for example. You already know that 6x5=30. That is you know if you had six piles of dragon eggs and each pile had five dragon eggs in it, altogether you would have thirty dragon eggs. At the same time, without even having to learn it you also know that 5x6=30. Yup five piles of dragon eggs with six eggs in each also means 30 altogether. And actually you already know two other things as well. You know that if you had 30 eggs and you put them in six equal piles there would be 5 eggs in each. In maths that looks like this: 30/6=5. That's division. You're dividing dragon eggs into equal piles. You also know that if you had 30 eggs and put them in five equal piles there would be six eggs in each. That looks like 30/5=6. That's division too! You see you know that 6 and 5 and 30 have a special way that they relate to each other. It's pretty good going really. Just by learning one thing i.e. 6x5=30 you ALSO know three other things 6x5=30 therefore 5x6=30 therefore 30/5=6 therefore 30/6=5! It's the same for every thing you learn in the multiplication table, learn one fact and you get an extra three thrown in for free. Trust me, I'm a doctor. Love RR 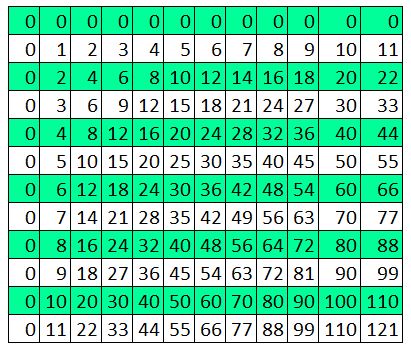 So if we look at the two times table, which as we know is also the list of all the even numbers you'll notice that all the even numbers end in zero, two, four, six, or 8 0, 2, 4, 6, 8. Even numbers always end in 0,2, 4 , 6 or 8. Here's a cool thing, if you times an even number by anything the answer is ALWAYS an even number. Let's take a look. A quick sneaky preview of all the even numbers in the times table. I've highlighted the times table for all the even numbers and you'll see there's only even numbers. This is very handy. If you are ever wondering does 4x4=16 or does 4x4 =46519 you'll know it must be 16 because 16 is an even number and 46519 is an odd number and even numbers multiplied by anything are always even. UNFORTUNATELY the same rule does NOT apply for odd numbers. If you multiply odd numbers by other numbers they can end up odd or even. But there is an odd rule about odd numbers An odd rule about odd numbers An odd number multiplied by an odd number is always odd. Whoa. That's ODD. You better and go and demand a chocolate milkshake from whatever adult is closest to you while you think about that. I only just figured that out. I think maybe I knew it when I was nine but I forgot it. I have to check it for myself. Yup, there we go, all the odd times odd numbers are odd. Excellent.
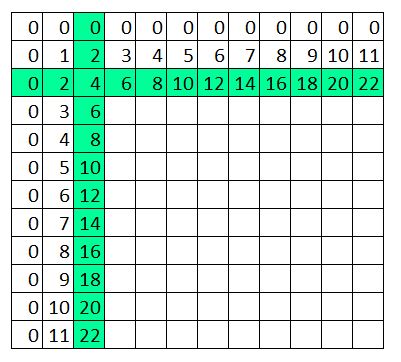
Here's a little rhyme that doesn't rhyme to help you remember. Even times anything is EVEN Odd times odd is ODD Yes, I KNOW you know the TWO times table. And you know the zero and the one times table. But we have to do things in order otherwise everything will go wonky. It will run around like an orange knitted pig saying wonk wonk, wonk wonk, wonk wonk. I have already told you that ONE times Something = the Something can be written in a special code like this 1a=a Well the two times table looks like this: 2a=(a+a) and you will be astonished to discover that with the three times table it would be 3a=(a+a+a) Doing the two times table is all about doubling. You take whatever number you need to times by two and you double it. Doubling is a very good thing to keep thinking about because it is useful in all sorts of ways. A few of which I will tell you about later. And because you already know the two times table you actually already know a bunch of other things. Doing the two times table is also just listing all the even numbers and missing out the odd numbers. 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 Knowing even numbers is very useful as well. There's quite an interesting thing to know about even numbers and the times tables. I'll talk about it in my next blog post. O-KAY, o-KAY! I can hear you say. I already know my ONE times table. It’s easy. Yeah Yeah, I know you know it. So this will be really short. One times anything is itself. One times two trillion is two trillion. One times seven is seven. There’s a special code people use to explain maths and we can use it to describe the one times table. 1a=a In this code a can mean whatever number you want. And in this code if you’re multiplying things you don’t put the times sign "x" in. You just put the numbers next to each other. _______________ Here’s a secret trick I discovered which will be quick way to remind you of the one times table. It will save you a lot of time. Take whatever number you are multiplying by one, multiply it by 345, add four hundred and sixteen, divide by eight, triple it, times by zero and add your number and BINGO you have your number times one. For example 8 x 345 =2760 2760+416=3176 3176/8 = 397 (that's a divided by sign, have you done them yet?) 397 x 3 (or tripled) = 1191 1191 x 0 = 0 (see previous blog post) 0 + 8 = 8 AMAZING! Now you need never worry about the one times table again.
You’re welcome. Love, The Fat Lady  Dear Maggie Do you know that where Astrid Lindgren is from Pippi Longstockings is actually Pippi Langstrum but there's a tiny tiny weeny wee circle above the a, I think you need a special keyboard to put it there because I am looking at the keyboard and I can't see one. I just looked behind the keyboard but I couldn't see it there either. Do you think Tuesday ate it? I think that tiny weeny little circle probably means you pronounce the a in a special Swedish kind of way. I like that scene in Pippi Longstockings when she decides to go to school because she wants to learn multiplikation though I thought she also said multiplifikation and maybe other things as well. Anyway, I know you're not a fan of Multiplation tables or even Multi-cake-nation tables even if they were tables covered in Red Velvet Cakes, and maybe numbers annoy you a bit so I thought I would tell you all the interesting things about Multi-fraction Tables I could in words because you like words. I am going to do these Extra-Special-Scrumptious-Things on Tables in separate blog thingees because otherwise this blog thingee will get t o o o o l o o o o o o o o o o n g !  Dear Maggie, Did you know you that you know one part of the 5-billion-and-eighteen times table? Yup, you know 5-billion-and-eighteen times zero. It's ZERO. Because as you already know Zero times anything is ...*exciting pause* ...*drum roll* ...*Maggie rolls her eyes and says 'Very Interesting!' in a tone that means not very interesting at all* ... ... ... ZERO. This is because if you had NO (or ZERO or 0) red velvet cakes and then you had no red velvet cakes again (that makes TWO times ZERO red velvet cakes you would still have ZERO red velvet cakes. And if you had NO red velvet cakes 5-billion-and-eighteen times over you would still have ZERO red velvet cakes and Nanny Piggins wouldn't be very happy about that, would she? And also of course all the number of red velvet cakes in between 1 & 2 & times ZERO also equal ZERO. Here is my picture of 5 billion and eighteen red velvet cakes times ZERO all crammed onto a table. I hope this is helpful.  Very complicated picture of the equation 5,000,000,018 x 0 Very complicated picture of the equation 5,000,000,018 x 0 Love Mama / Mrs Loolupants Selected Poems, Fleur Adcock. Oxford University Press, 1983. Being a girl is dangerous. I don't just mean we are vulnerable to danger, but that we are, ourselves, dangerous, capable of causing great damage to ourselves and others. We, especially in those years we are changing into women, live in danger, where danger is the vibrating state we occupy. I started thinking tonight about Fleur Adcock's Selected Poems which I first read at 15. I remembered the dark green cover and how the spine looked on my parents' bookshelf. The slim sitting room one with the cut out hearts and tidy shelves of Penguins. Have I made up the moment of discovery? Of pulling the book from the shelf, of curling in the large brown chair with the ribbed pattern that would leave its tribal marks on me? The book must have come alive to me then, something that breathed and beat so that next time I came to the shelf I would recognise it. It would hum when I entered the room. It was my mother's book but became mine in the way any book is claimed as intimate property by obsessed readers. I wonder if it in turn claimed me, lodging its shards in my ears and brain and heart, because it was the first book of poetry I really read. A book I read for sheer pleasure but also I read and reread wanting to understand how Fleur Adcock had done it. I don't know if that is peculiarly a budding poet's reading, or if that is the nature of all close reading of poetry. That the thrill of a good poem is watching it run but also holding it in your lap, seeing the bones and muscles move beneath the pelt, smelling its oily springed wool. Understanding how it all fits together. Do teenagers, or at least the kind I was, gravitate towards poetry because the best of it is transformative in the same way adolescence is? Good poetry allowing us not just to see the capacity of the poet, but our own capacities. A transformation from passive childlike recipients of the word and the world, to readers active, engaged and creative in our own right. I think about how it's not just writers who are dangerous, with their strange ability to conjure mountains and moods, but readers too. There is a moment, when we get poems, if we get them, where we are not having something done to us by the poem, but we are doing something to the poem. A good poem, that we have read and understood, can give us a sense of mastery, perhaps what a musician feels when she plays fluently, for the first time, a difficult piece of music. It is a long time since I have opened Adcock's book and when I do it is with great affection as phrases I have loved for 30 years float up off the page out to me, triggering the same pings of pure pleasure as they did on my first encounter with them. ichnueman flies have got in It is 5 a.m. All the worse things come stalking in and stand icily about the bed looking worse and worse and worse ...and tiptoes in sandals that softly waffle-print the dusty floor 'Oblivian, that's all, I never dream' he said – proud of it, another immunity 'Will I die?', you ask. And so I enter on That dutiful exposition of that which you Would rather not know. Phrases which are part of my own history, which have been absorbed into my sense of the musicality of language, and which have shaped how I have read poetry ever since. And now, on this return, an added richness because I see the connection between Adcock and others. Her poems about the death of old lovers feel close to Lauris Edmond's. There is something of Adcock's parental ambiguity in Helen Lehndorf's gothic works of domesticity. I've just read Adcock's sister Marilyn Duckworth's 1970 book Over the Fence is out, and I see shared insight into the complexities of male violence against women. As Helen Heath explores in her poetry the intersections between human and synthetic worlds, I know she should read 'Gas', Adcock's speculative sequence on involuntary cloning. She sees with my imperfect vision, she wears my finger-prints; she is made from me. If she should break the bones I gave her, if disease should invade her replicas of my limbs and organs, which of us is betrayed? On re-examining the book I encounter again Adcock's formidable combination of cool formality and passion. Intense feelings bounded by guarded line and graceful rhythms. Feelings constrained, almost to the point of repression. The words seem to rebel against their dignified imprisonment, amplifying their potency. With Adcock I am always coming and going. Sailing so close to the poems' narrator our skins touch, feeling so close it as is if I understand the warm workings of another's body. This claustrophobia is not always, or even often, pleasant. If I were to touch you I should feel Against my fingers fat, moist worm-skin. I sail from here to a glittering windy world of wry distance, observation, salty intelligence. From Adcock I learned it was possible to write intimately without gushing, to write seriously without being doughy. The arts of deft restraint. This darkness has a quality That poses us in shapes and textures, One plane behind another, Flatness in depth. Your face; a fur of hair, a striped Curtain behind, and to one side cushions; Nothing recedes, all lies extended. I sink upon your image. What surprised me, when I found the battered copy of the never returned book on my shelf in a different room, in a different house, was how dangerous this book is. It's why I started thinking about danger. I wanted to find a belt and wrap it around the book like you must do with Harry Potter's Monster Book of Monsters to avoid being bitten. Selected Poems has tigers and rapists, maggots and prowlers, kitten killing mothers and exile, skinned dogs and nightmarish realisations. It was obscure, but glancing towards the end she guessed that killer, and lover and doctor were the same; proving that things are ultimately what they seem. Every hopeful poem about mothering and childhood in this book contains within it a moment of dying. Every relationship poem contains the demise of the relationship. It's a frightening book. Slightly hellish in its vision, full of serious and very adult truths. It's brutal and beautiful and honest. No wonder I loved it then, love it still. Look, children, the wood is full of tigers, warns Adcock. They've eaten all the squirrels. They want you, And it's no excuse to say you're only children. No one is on your side. What will you do? |
Categories
All
Archives
March 2023
(C) Copyright 2012, Mrs Loolupants, All Rights Reserved.
|






 RSS Feed
RSS Feed
